Tesi di Laurea in Ingegneria

Approccio numerico per la soluzione del moto parabolico in presenza di attrito viscoso

Lezione del 26 - III - 1

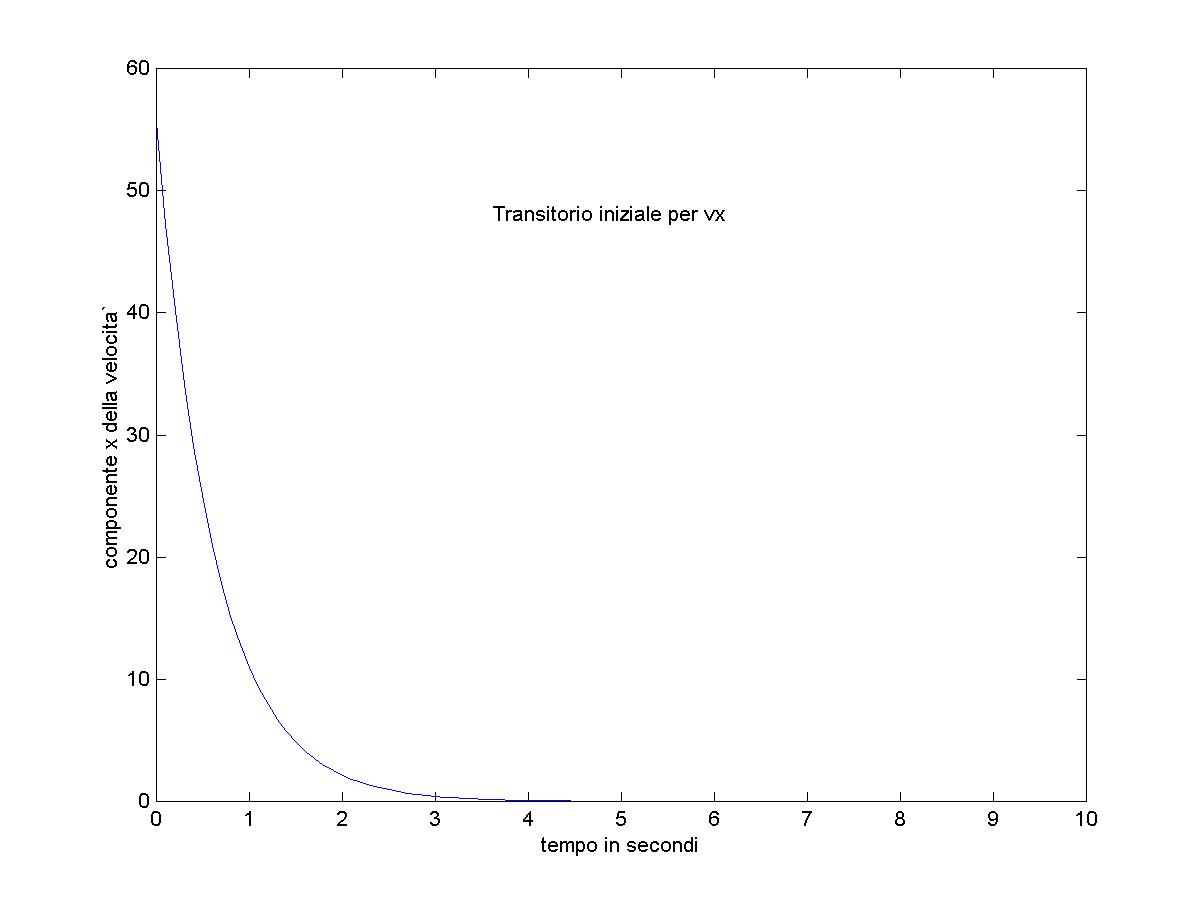
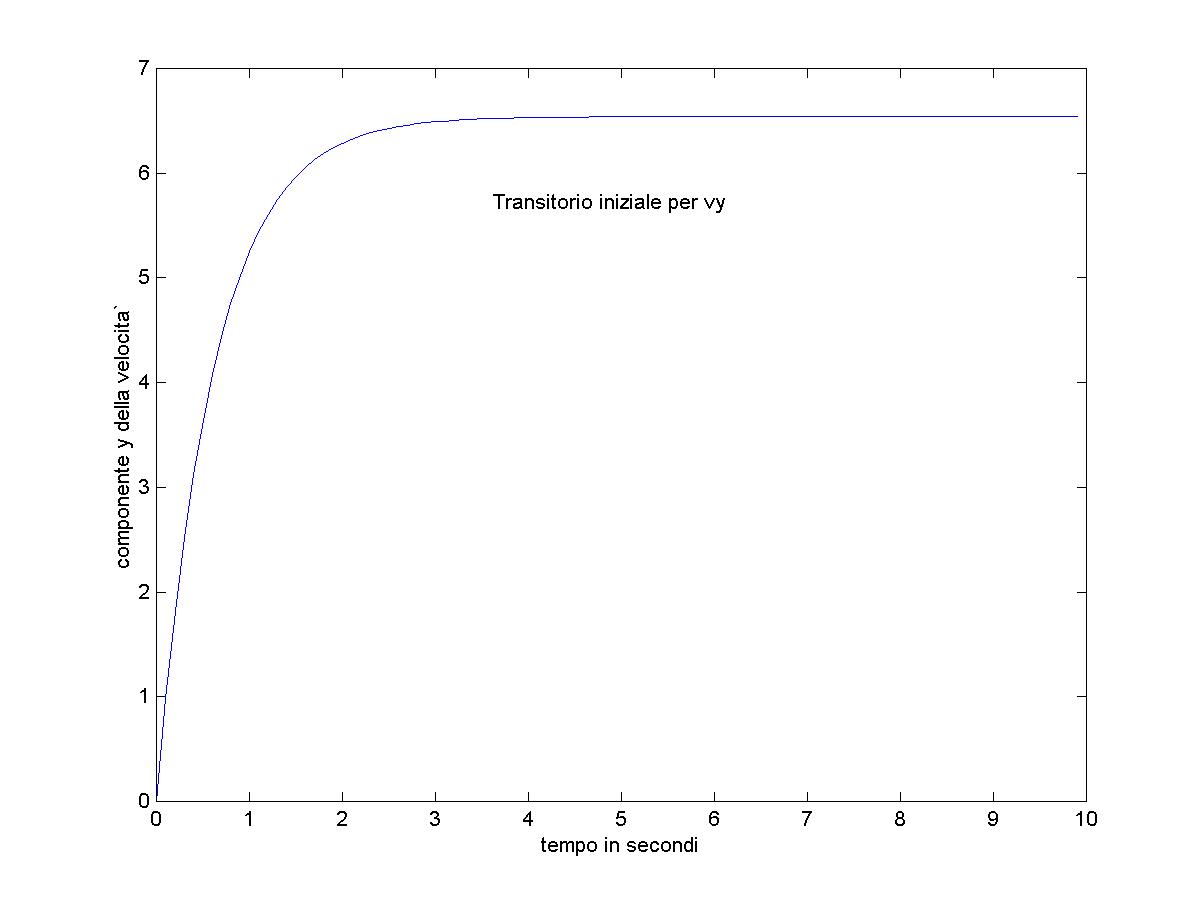
% modello numerico del moto con attrito viscoso
%P. Villoresi 25 - 3 - 1

x(1)=0;         %posizione e velocita` iniziale in X
vx(1)=55.6;

y(1)=0;         %asse y verso il basso; 
vy(1)=0;                %posizione e velocita` iniziale in Y

b=15;                   %costante della forza viscosa Fa = - b v
m=10;                   %massa
g=9.81;
dt=0.1;         %passo temporale

passo=1;
while y<3000    %quota finale, corrispondente al suolo
   
   vx(passo+1) = vx(passo) - b / m * vx(passo) * dt;
   x(passo+1) = x(passo) + vx(passo) * dt;
   
   vy(passo+1) = vy(passo) + ( g - b / m * vy(passo)) * dt;
   y(passo+1) = y(passo) + vy(passo) * dt;
   
   passo=passo+1;
   
end

tempocaduta= passo * dt
xfinale = x(passo)

%       RISULTATI

% tempocaduta =   459.5000 s

% xfinale =    37.0667 m

Risultati numerici nella prima parte del calcolo, ossia nel transitorio iniziale. Ogni riga corrisponde all'avanzamento di un passo temporale, quindi ad un tempo di 0.1 s successivo alla riga precedente.

        vx                 x                    vy                y
        
  55.60000000000000                  0                  0                  0
  47.26000000000000   5.56000000000000   0.98100000000000                  0
  40.17100000000000  10.28600000000000   1.81485000000000   0.09810000000000
  34.14535000000000  14.30310000000000   2.52362250000000   0.27958500000000
  29.02354750000000  17.71763500000000   3.12607912500000   0.53194725000000
  24.67001537500000  20.61998975000000   3.63816725625000   0.84455516250000
  20.96951306875000  23.08699128750000   4.07344216781250   1.20837188812500
  17.82408610843750  25.18394259437500   4.44342584264063   1.61571610490625
  15.15047319217187  26.96635120521875   4.75791196624453   2.06005868917031
  12.87790221334609  28.48139852443594   5.02522517130785   2.53584988579477
  10.94621688134418  29.76918874577055   5.25244139561167   3.03837240292555
   9.30428434914255  30.86381043390497   5.44557518626992   3.56361654248672
   7.90864169677117  31.79423886881922   5.60973890832943   4.10817406111371
   6.72234544225549  32.58510303849634   5.74927807208002   4.66914795194665
   5.71399362591717  33.25733758272188   5.86788636126802   5.24407575915466
   4.85689458202959  33.82873694531360   5.96870340707781   5.83086439528146
   4.12836039472515  34.31442640351656   6.05439789601614   6.42773473598924
   3.50910633551638  34.72726244298908   6.12723821161372   7.03317452559085
   2.98274038518892  35.07817307654072   6.18915247987166   7.64589834675223
   2.53532932741059  35.37644711505961   6.24177960789091   8.26481359473939

Risultati numerici nella parte finale del calcolo, ossia quando si ragguinge il suolo (y = 3000 m).


  1.0e+003 *
   0.00000000000000   0.03706666666667   0.00654000000000   2.99357599999998
   0.00000000000000   0.03706666666667   0.00654000000000   2.99422999999998
   0.00000000000000   0.03706666666667   0.00654000000000   2.99488399999998
   0.00000000000000   0.03706666666667   0.00654000000000   2.99553799999998
   0.00000000000000   0.03706666666667   0.00654000000000   2.99619199999998
   0.00000000000000   0.03706666666667   0.00654000000000   2.99684599999998
   0.00000000000000   0.03706666666667   0.00654000000000   2.99749999999998
   0.00000000000000   0.03706666666667   0.00654000000000   2.99815399999998
   0.00000000000000   0.03706666666667   0.00654000000000   2.99880799999998
   0.00000000000000   0.03706666666667   0.00654000000000   2.99946199999998
   0.00000000000000   0.03706666666667   0.00654000000000   3.00011599999998

Rappresentazione grafica del transitorio di vx e vy

dr. Paolo Villoresi

pavil@dei.unipd.it