Eserciziario di Reti di Calcolatori
Università degli Studi di Padova, a.a. 2004-05, prof. Satta
Esercizio n.3 - Compito 25/06/2004
Testo:
Si deve trasmettere il messaggio 1110010101 (10 bit) utilizzando l'algoritmo CRC per la rilevazione d'errore ed il polinomio x5+x2+1.
- Determinare il messaggio trasmesso.
- Supponendo che il secondo bit più significativo venga invertito nella trasmissione, determinare se e come il ricevitore sia in grado di rilevare tale errore.
Riportare i passaggi intermedi per tutte le risposte.
Risoluzione:
Il polinomio usato per il rilevamento degli errori ha grado k=5 e corrisponde alla sequenza 100101.
a.
Calcoliamo la sequenza da trasmettere P(x):

Il primo termine viene calcolato eseguendo lo shift a sinistra del messaggio di k posizioni. M(x) * x5 = 111001010100000
Il secondo termine è il resto della divisione 
111001010100000
100101
0111000
100101
0111011
100101
0111100
100101
0110011
100101
0101100
100101
00100100
100101
00000100
________
100
=> R(x) = 100
Trovo quindi P(x):
P(x) = 111001010100000 - 100 = 111001010100100
tenendo presente che la sottrazione in binario corrisponde all'operatore XOR.
b.
Invertendo il secondo bit più significativo di P(x), si ottiene che il messaggio ricevuto è 101001010100100
Devo verificare che il ricevitore si accorga dell'errore eseguendo la divisione del messaggio ricevuto per C(x) e controllando se il resto sia nullo o meno; nel secondo caso significa che l'errore viene rilevato.
101001010100100
100101
00110001
100101
0101000
100101
00110110
100101
0100110
100101
000011100
_________
11100
R(x) = 11100
Il resto è diverso da 0, quindi l'errore viene rilevato e verrà richiesta la ritrasmissione del messaggio.
Testo:
Supponete che da una linea arrivi la seguente sequenza di bit:
1101011111010111110010111110110
Mostrate il frame risultante dopo la rimozione dei bit interposti. Indicate anche errori eventualmente presenti nel frame.
Risoluzione:
I protocolli orientati al bit con sentinella prevedono l'uso di una speciale sequenza di bit, denominata sentinella appunto, che permette di discriminare l'inizio e la fine di un frame dal resto dei dati. La sentinella è:
01111110
Può accadere che tale sequenza di bit faccia parte dei dati da trasmettere; questo causa errori in fase di ricezione. Per permettere una rilevazione corretta dei confini del frame si rende dunque necessaria una operazione speciale denominata "bit stuffing". In fase di trasmissione i dati vengono verificati e, se viene rilevata la sentinella, prima dell'ultimo "1" viene arbitrariamente inserito uno "0". Il ricevitore effettua lo stesso controllo; quando
rileva la sequenza
011111
verifica il bit successivo:
- se è uno "0" va certamente eliminato (si tratta del bit inserito dalla sorgente);
- se è un "1" va controllato il bit successivo:
- se è uno "0" si tratta di una sentinella e va riconosciuta come tale;
- se è un "1" si è verificato un errore.
Nel caso proposto dall'esercizio non si è verificato nessun errore e non è presente alcuna sentinella; i bit da eliminare occupavano le posizioni indicate:
1101011111 1011111 01011111 110
^ ^ ^
Testo:
Supponete di voler inviare dati usando il protocollo di framing BISYNC e che gli ultimi due byte dei dati sia DLE e ETX.
Quale sequenza di dati dovrebbe venire trasmessa subito prima del CRC?
Risoluzione:
Il byte ETX è un carattere speciale usato dal protocollo BISYNC per segnalare la fine di un frame (End of TeXt). Se questo carattere si trova nei dati la sorgente deve curarsi di farlo precedere da un altro carattere speciale, denominato DLE (Data Link Escape); in questo modo il ricevente che trovi un carattere DLE seguito da ETX sa che DLE va eliminato e che ETX non è un segnale di controllo ma fa parte dei dati.
Il protocollo inoltre prevede che se i dati contengono un carattere DLE va preposto anche ad esso un ulteriore DLE. La tecnica fin qui esposta è denominata "character stuffing".
Nel caso dell'esercizio la soluzione è:
DLE DLE DLE ETX ETX
in cui il primo e il terzo DLE rappresentano caratteri di escape, cioè inseriti dalla sorgente, mentre il secondo DLE ed il primo ETX sono dati da trasmettere.
L'ultimo ETX è il carattere di controllo che chiude il frame.
Testo:
Dimostrate che la parità bidimensionale consente la rilevazione di tutti gli errori di 3 bit.
Risoluzione:
La parità unidimensionale o semplice consiste nell'aggiunta di un bit ad una stringa più o meno estesa di bit di dati (solitamente 7). La parità può essere di tipo pari (even) o dispari (odd) e il valore del bit di parità viene calcolato in questo modo:
- even: il bit assume valore "1" se e' necessario per rendere pari il numero totale di bit a "1", valore "0" altrimenti;
- odd: il bit assume valore "1" se e' necessario per rendere dispari il numero totale di bit a "1", valore "0" altrimenti;
La parità bidimensionale considera i bit dei dati suddividendoli in righe e colonne; viene poi effettuato il calcolo di un bit di parità per ogni riga e per ogni colonna ottenuta. I bit di parità costituiscono così, a loro volta, una riga (dai calcoli sulle colonne) e una colonna (dai calcoli sulle righe) sulle quali avviene un ulteriore calcolo di parità unidimensionale, ottenendo un solo ultimo bit di parità (vedere fig. 2.16 pag. 77 del libro
di testo).
Per dimostrare quanto chiesto dall'esercizio dobbiamo verificare che per ogni possibile posizione dei 3 bit di errore nella "matrice" di dati il controllo di parità fatto dal ricevitore fallisce (cioè rileva un errore).
Cosideriamo le possibili disposizioni dei bit errati nelle righe. Si presentano tre casi:
-
I 3 bit errati sono tutti nella stessa riga
In questo caso è chiaro che il controllo di parità fallisce: due bit hanno i loro valori invertiti, e ciò non è rilevato dalla parità, ma un terzo bit sulla stessa riga è invertito; questo garantisce che l'errore venga rilevato perché il bit di parità di riga à certamente sbagliato. -
I 3 bit errati appartengono a tre righe diverse
Questo caso comporta la rilevazione dei tre distinti errori: si avranno tre parità di riga sbagliate. -
I 3 bit errati appartengono a due righe diverse
La rilevazione dell'errore avviene anche in questa situazione. I due bit invertiti che appartengono alla stessa riga sfuggiranno al controllo di parità di riga. Il terzo bit sbagliato invece, essendo l'unico della sua riga, sarà certamente individuato.
Il ragionamento da fare per quanto riguarda la posizione degli errori nelle righe è del tutto analogo. L'unico caso "particolare" è che i 3 errori si presentino in un bit di dati e nei due bit di parità delle sue riga e colonna. In questa evenienza il controllo di parità rileva comunque l'errore: ad essere sbagliato sarà il bit di parità che viene calcolato per ultimo (ved. spiegazione).
In questo modo abbiamo provato che tutte le possibili disposizioni di 3 bit errati comportano almeno un errore di parità quando il ricevitore procede alla verifica. Aggiungiamo inoltre una osservazione. Il ragionamento esposto si estende anche ai bit di parità stessi: in altre parole se uno o più dei 3 errori interessa/no proprio i bit di parità il controllo mostra ugualmente la situazione di errore.
Testo:
Dimostrare che la parità bidimensionale fornisce al ricevitore informazioni sufficienti per correggere qualsiasi errore di 1 bit (nell'ipotesi che il ricevitore sappia che c'è un solo bit errato), ma non un errore qualsiasi di 2 bit.
Risoluzione:
La parità bidimensionale è basata sulla parità semplice (unidimensionale), che solitamente comporta l'aggiunta di un bit extra ad un codice a 7 bit per rendere bilanciato il numero di valori 1 nel byte. La parità bidimensionale effettua un calcolo simile per ciascuna posizione di bit in tutti i byte contenuti nel frame.
Ciò produce un byte aggiuntivo di parità per l'intero frame, in aggiunta al bit di parità presente in ciascun byte. Nei casi in cui durante la trasmissione venga inserito nel messaggio un solo errore, il controllo a doppia parità ( o parità bidimensionale ) consente di individuare l'esatta posizione di tale errore e quindi di correggerlo. Con questo metodo di controllo d'errore si riesce infatti a capire in quale byte del messaggio si trova il bit errato
ed in quale posizione si trova all'interno del byte. Dalle figure sotto riportate si può vedere, in un semplice esempio, quanto sopra descritto.
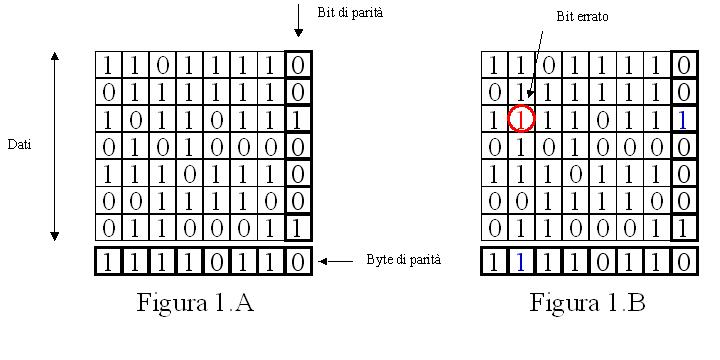
La figura 1.A mostra il messaggio corretto, inviato dal mittente con i relativi bit e byte di controllo.
La figura 1.B mostra il messaggio ricevuto dal destinatario.
Eseguendo un nuovo controllo di parità e confrontando il risultato con i bit di parità contenuti nel messaggio ricevuto si notano due discordanze. I due bit di controllo discordanti con il contenuto del messaggio (in blu) indicano in modo univoco la posizione del bit errato (in rosso) qualsiasi essa sia all'interno del messaggio.
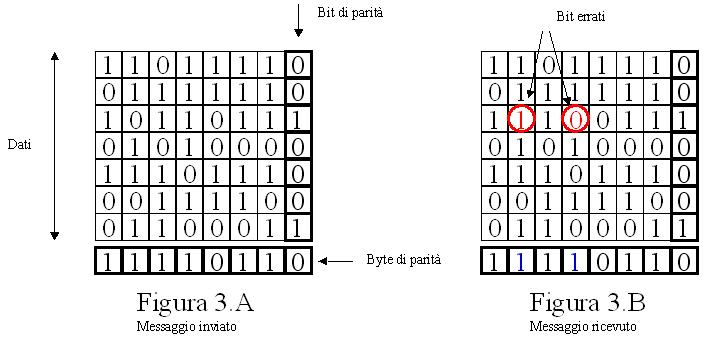
Nel caso in cui vengano trasmessi in modo errato due bit del messaggio, il controllo a parità bidimensionale non sempre è in grado di indicare le posizioni occupate dai bit errati nel messaggio. Facendo riferimento alle figure riportate sopra si può dire che il controllo a doppia parità è in grado di indicare le posizioni dei due bit errati solo se essi occupano due diverse colonne e due diverse righe (i due bit non sono allineati figure 2.A e 2.B). In
tutti gli altri casi (figure 3.A e 3.B) il controllo può solo indicare che il messaggio ricevuto contiene due bit errati senza poter dire qual è la loro posizione.

Testo:
Supponete di voler trasmettere il messaggio 11001001 e di volerlo proteggere dagli errori usando il polinomio CRC x3 + 1.
-Usate la divisione in colonna di polinomi per determinare il messaggio da trasmettere.
-Supponete che il bit più a sinistra del messaggio cambi di valore per effetto di rumore sulla linea di trasmissione. Qual è il risultato del CRC eseguito dal ricevente? Come fa il ricevitore a sapere che c'è stato un errore?
Risoluzione:
a.
Dato che il grado del polinomio C(x) è pari a tre dobbiamo aggiungere al messaggio, corrispondente al polinomio M(x), 3 zeri alla fine ottenendo il polinomio T(x) = M(x) * x3. Fatto questo dobbiamo dividere questultimo per 1001 (che corrisponde al polinomio C(x) = x3 + 1).

Ora dobbiamo sottrarre a T(x) il resto della divisione ricordando che la sottrazione tra due polinomi corrisponde allo XOR tra i polinomi. Il risultato di tale operazione, P(x), sarà il messaggio che verrà effettivamente trasmesso.

b.
Il messaggio giunto al ricevente sarà 01001001011. Dividendo questultimo per C(x) otterremo il resto R(x). Per come è stato calcolato P(x) dal mittente si può dire che:
-
un valore nullo relativo a R(x) indica che il messaggio è stato trasmesso correttamente senza introduzione di errori;
-
un valore di R(x) diverso da zero indica che il messaggio non è stato trasmesso correttamente e che quindi contiene degli errori.
Nel nostro caso si ha :

Come previsto, il resto R(x) è diverso da zero dato che durante la trasmissione il bit più a sinistra del messaggio ha cambiato valore.
Testo:
Indicate in dettaglio come aggiungere il controllo di flusso al protocollo sliding window, usando le conferme (ACK) per veicolare informazioni addizionali allo scopo di ridurre il valore di SWS quando il ricevitore esaurisce lo spazio disponibile nel buffer. Illustrate il vostro protocollo con un diagramma temporale della trasmissione, nell'ipotesi che SWS e RWS valgano inizialmente 4, che la velocità della linea sia infinita e che il ricevitore possa creare nuovi buffer al ritmo
di uno al secondo (per cui il collo di bottiglia è proprio il ricevitore). Mostrate cosa accade agli istanti T=0, T=1, ... , T=4 secondi.
Soluzione:
Per poter aggiungere il controllo di flusso è necessario che il ricevitore dica al mittente quanti frame puo' ancora ricevere (cioè quant'è il buffer a disposizione). Per questo motivo gli ACK non porteranno solamente le informazioni relative al numero di sequenza del frame confermato, ma anche una indicazione sulla variazione dello spazio nel buffer del ricevitore (che si traduce con una diminuzione della SWS). Indicheremo con ACK[ SeqNum, R = x] la conferma del
frame con numero di sequenza uguale a SeqNum, che modifica la SWS di R (x può assumere i seguenti valori: -1 se la SWS viene ridotta di 1, 0 se la SWS non viene modificata, +1 se la SWS viene aumentata di 1).
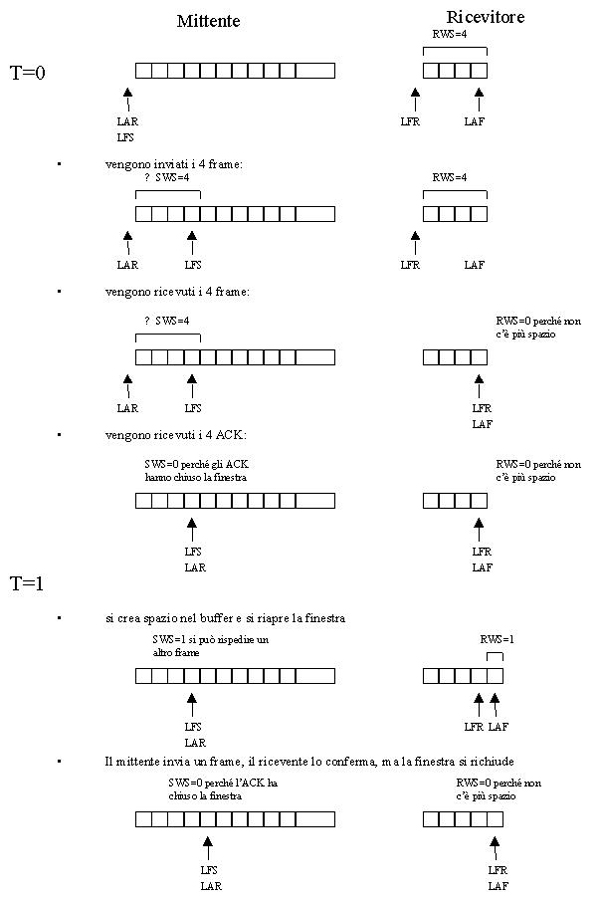
T=0 : siccome la velocità della linea è infinita, il tempo di trasmissione di qualsiasi frame è pari a 0, quindi una conferma arriverà dopo un tempo pari a RTT da quando è stato trasmesso il frame. Siccome il collo di bottiglia è nel ricevitore, possiamo sicuramente affermare che gli ACK arriveranno in un tempo molto inferiore a 1 secondo (cioè RTT << 1 s).
Quindi all'istante T=0 partiranno 4 frame (la dimensione della SWS) e ritorneranno gli ACK: ACK[1, R = -1]; ACK[2, R = -1]; ACK[3, R = -1]; ACK[4, R = -1]. Questi causeranno una riduzione della SWS tale da farla chiudere (SWS=0).
A causa della chiusura della SWS il mittente non potrà più inviare niente fino a quando non succede qualcosa (nel nostro caso stiamo aspettando che il ricevitore ci dica che ha dello spazio nel buffer).
T=1: si crea dello spazio nel buffer. Siccome il mittente non può ripartire da solo, è necessario che il ricevitore segnali la disponibilità di spazio con un ACK[4, R = +1]. La dimensione della SWS cresce così a 1 e diventa possibile inviare il frame con SeqNum = 5. Il ricevitore manda ACK[5, R = -1] e la SWS torna a 0, bloccando nuovamente il mittente.
T=2: fino all'istante T=4 si ripetono gli stessi meccanismi del punto precedente, cambiano solamente i SeqNum dei frame. Il ricevitore invia ACK[5, R = +1], il mittente invia il frame con SeqNum = 6, il ricevitore manda ACK[6, R = -1], SWS va a 0.
T=3: Il ricevitore invia ACK[6, R = +1], il mittente invia il frame con SeqNum = 7, il ricevitore manda ACK[7, R = -1], SWS va a 0.
T=4: Il ricevitore invia ACK[7, R = +1], il mittente invia il frame con SeqNum = 8, il ricevitore manda ACK[8, R = -1], SWS va a 0.
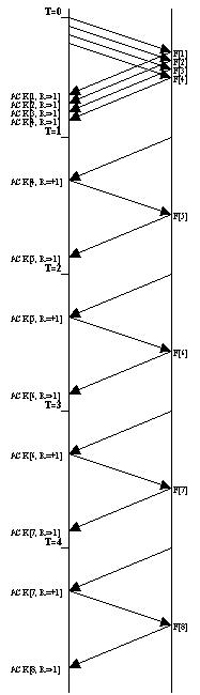
Osservazione: se uno degli ACK che riaprono la finestra viene perso, il ricevitore è comunque convinto che il messaggio sia arrivato, ma il mittente è ancora bloccato. Di conseguenza è necessario implementare un meccanismo di affidabilità per quei tipi di messaggi, per esempio utilizzando delle temporizzazioni.
Testo:
Tracciate un diagramma temporale per l'algoritmo sliding window con SWS = RWS = 3 frame, nelle due situazioni seguenti. Usate un intervallo di timeout circa uguale e 2 x RTT. a) Il frame 4 viene perduto. b) I frame dal 4 al 6 vengono perduti.
Soluzione:
Facciamo riferimento alle figure che seguono.
a)
Inizialmente le finestre della sorgente e del ricevente sono nella stessa posizione: entrambe comprendono i frame 1, 2 e 3; questo vuol dire che il trasmettitore puo' iniziare a spedire immediatamente i primi tre frame, come il ricevitore si aspetta.
Appena il ricevente memorizza i tre frame invia gli acknowledgement A[1], A[2] e A[3]; successivamente ad ogni invio la finestra del ricevente avanza di una posizione, fino a comprendere i frame F[4], F[5] ed F[6] che dovranno essere ricevuti.
Il processo di trasmissione procede con la sorgente che alla ricezione di ciascun ACK fa avanzare la propria finestra di una posizione; in questo modo invia i frame successivi, vale a dire F[4], F[5] ed F[6], immediatamente dopo la ricezione di A[1], A[2] e A[3], rispettivamente.
L'esercizio prevede che il frame F[4] venga perso.
A questo punto il ricevente memorizza i frame F[5] ed F[6], ma non invia alcun ACK: il protocollo sliding window prevede infatti che i frame ricevuti "non in sequenza", come F[5] ed F[6], vengano memorizzati, ma non confermati alla sorgente.
La mancata ricezione di A[4] comporta, nel trasmettitore, lo scadere del timeout su F[4]; a questo punto il trasmettitore ritrasmette il frame.
Come si nota dalla figura la ritrasmissione avviene appunto dopo la scadenza del timeout, vale a dire 2 x RTT.
Il ricevitore risponde, appena ricevuto F[4], inviando un ACK cumulativo per tutti i frame ricevuti fino a questo momento: invia dunque A[6]; la finestra del ricevitore avanza di tre posizioni e comprende ora F[7], F[8] ed F[9].
La situazione di errore sarebbe risolta, ma rimane da chiarire un punto; poco dopo lo scadere del timeout per F[4] scadono infatti anche quelli per F[5] ed F[6]. Il trasmettitore si comporta come con F[4], provvedendo alla ritrasmissione dei frame in oggetto. Il ricevitore pero', leggendo i numeri di sequenza dei frame, si rende conto di averli gia' memorizzati e li elimina.
La trasmissione continua nel momento in cui il trasmettitore vede A[6]; la sua finestra avanza di tre posizioni e il successivo gruppo di frame trasmessi e' F[7], F[8] ed F[9].
b)
La seconda parte dell'esercizio prevede che vengano persi F[4], F[5] ed F[6].
Il comportamento del sistema e' del tutto simile a quello esposto nel caso precedente; questa volta pero' il ricevitore non memorizza alcun frame fuori sequenza.
Il trasmettitore aspetta di ricevere A[4]; allo scadere del timeout ripete l'invio di F[4]. Il ricevente risponde con A[4], che questa volta non e' un acknowledgement cumulativo, e fa avanzare la sua finestra di una posizione.
Prima che A[4] arrivi alla sorgente scadono anche i timeout di F[5] e di F[6], ed avvengono le loro ritrasmissioni.
Il ricevente risponde come al solito con A[5] e A[6], e facendo avanzare di volta in volta la sua finestra.
Quest'ultima, per quanto riguarda il trasmettitore, rimane ferma fino alla ricezione di A[4] che la fa avanzare di una unita', provocando la trasmissione immediata di F[7]; la successiva ricezione di A[5] e A[6] provoca effetti analoghi.
La comunicazione da qui in avanti continua normalmente.

Aggiungiamo alcune osservazioni.
E' possibile modificare il protocollo sliding window in modo da renderlo meno conservativo; in particolare e' possibile pensare che allo scadere del timeout per F[4] venga ripetuto l'invio, ma la stessa cosa non avvenga per F[5] ed F[6].
Questa scelta puo' essere valida in alcune situazioni, in altre meno; nel caso a) di questo esercizio e' senz'altro una buona scelta: era stato perso il solo F[4] e ripetere l'invio anche di F[5] ed F[6] e' inutile.
Nel caso b) invece la scelta migliore e' quella di ripetere l'invio per tutti i frame.
Va pero' ricordato che in nessun caso il trasmettitore sa "in anticipo" quali frame sono stati persi: la scelta migliore dunque pare essere quella piu' banale di ripetere l'invio ad ogni timeout scaduto.
Un ragionamento che porta a conclusioni opposte e' il seguente: se non viene ricevuto un ACK puo' essere a causa di problemi di congestione della rete; la scelta migliore e' allora quella di minimizzare il traffico generato, cioe' ripetere l'invio del solo F[4].
Testo:
Mostrate la codifica 4B/5B e il conseguente segnale NRZI per la seguente sequenza di bit:
1101 1110 1010 1101 1011 1110 1110 1111
Risoluzione:
Supponendo che il segnale NRZI parta da 0:

Testo:
Con un protocollo di framing che usa l'interposizione di bit, mostrate la sequenza di bit trasmessa sulla linea quando il frame contiene la seguente sequenza di bit:
110101111101011111101011111110Contrassegnate i bit interposti.
Risoluzione:
Per trasmettere il frame con un protocollo ad interposizione di bit si inserisce uno 0 ogni volta che nella sequenza da trasmettere si incontrano cinque 1 consecutivi; la stringa effettivamente trasmessa è quindi:
110101111100101111101010111110110
^ ^ ^
Testo:
Nella codifica 4B/5B (Tabella 2.4). soltanto due delle parole di codice a 5 bit utilizzate terminano con due zeri. Quante sono le possibili sequenze di 5 bit (usate dal codice in esame oppure no) che soddisfano il requisito più stringente di avere al massimo un solo zero iniziale ed un solo zero finale? Esiste una corrispondenza tra tutte le sequenze di 4 bit e tali sequenze di 5 bit?
Risoluzione:
Le stringhe di 5 bit compatibili sono quelle corrispondenti ai numeri (<32) maggiori di 8 e non divisibili per 4, ovvero:
01001, 01010, 01011, 01101, 01110, 01111, 10001, 10010, 10011, 10101, 10110, 10111, 11001, 11010, 11011, 11101, 11110, 11111In tutto sono 18, quindi è sicuramente possibile stabilire una corrispondenza tra queste stringhe e tutte le stringhe di 4 bit.
Testo:
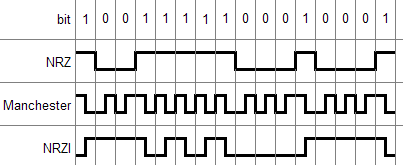
Mostrate, per lo schema di bit di figura 2.46, le codifiche NRZ, Manchester e NRZI. Ipotizzate che il segnale NRZI inizi con il valore basso.
Risoluzione:
Testo:
Mostrate la codifica 4B/5B e il conseguente segnale NRZI per la seguente sequenza di bit:
1110 0101 0000 0011
Risoluzione:
Supponendo che il segnale NRZI parta da 0:
